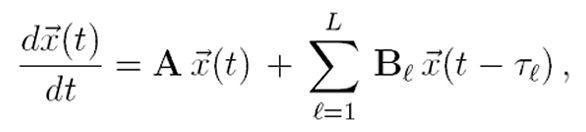A single delay example L = 1
This problem goes back to 1960s, and many milestones were covered in this problem.
Since there is only one delay, the stability chart is displayed along the 1-dimensional positive delay axis, where this axis is divided into infinitely many intervals. Any delay value in an interval either makes the TDS stable or unstable. Consequently, one can label the intervals as "stability favoring" or "instability favoring". The stability favoring intervals are also called as "stability intervals" or "stability pockets".
In the TDS presented, when L = 1, A = -2, B = -5, we find the following stability interval: 0 < = DELAY < 0.4326 sec., meaning that this dynamical system will be
stable when the delay is less than 0.4326 sec, and it will be unstable when the delay is greater than or equal to 0.4326 sec.
How could we compute the upper bound of the tolerable delay (so called "delay margin")? See our survey paper published in
SIAM Control and Optimization in 2006.