Northeastern University: 3D Concentrated Plasticity Macro Finite Element Formulation for CFT

Three-Dimensional Concentrated Plasticity "Macro" Finite Element Formulation for RCFT Beam-Columns

Principal Investigator:
Jerome F. Hajjar

Sponsors:
National Science Foundation
American Institute of Steel Construction
Northeastern University
University of Illinois at Urbana-Champaign
University of Minnesota

Graduate Students:
Mark Denavit
Jie Zhang
Cenk Tort
Steven M. Gartner
Brett C. Gourley
Jorge Grauvilardell
Narina Jung
Alexander O. Molodan
Paul H. Schiller
Cenk Tort
Jose Zamudio

Undergraduate Students:
Mahmoud Alloush
Tarik Ata Rafi
Rachel Back
Brian Beck
Wilfred Chan
Mark Chauvin
Kathryna Clarke
Steve Earl
Ryan Hopeman
Ezra Jampole
Saif Jassam
Michael Kehoe
Sarah Keenan
Angela Kingsley
Tyler Krahn
Susan K. La Fore
Gregory S. Lauer
Elisa Livingston
Brett Mattas
Steven Palkovic
Matthew Parkolap
Jill Pinsky
Alston Potts
Abdulrahman Ragab
Alexandra Reiff
Katherine A. Stillwell
Zhuanqiang Tan

EFT-idea

Typical Framing System Utilizing CFT Beam-Column

Macro Model Formulation

Top

Stress-resultant based formulation
Standard 3D beam element (line element)
12 degrees-of-freedom per element (shown below):

Elastic stiffness formulation assumes:
- Euler-Bernoulli beam-theory (e.g., sections which are initially plane and normal to the centroidal axis remain so during deformation)
- Cubic Hermetian shape functions
CFT element requires effective elastic rigidities, verified by comparison with experiments:
Axial: (EA)_CFT = (EA)_steel + (EA)_concrete
Flexural: (EI)_CFT = (EI)_steel + (EI)_concrete
Torsional: (GJ)_CFT = (GJ)_steel
Where: A = Cross-sectional area
             I = Moment of inertia
             J = Torsional constant
             E = Elastic modulus
             G = Shear modulus

Geometric stiffness formulation assumes:
- Small strain, moderate displacements, moderate rotations
- Updated Lagrangian formulation
- Captures all predominant geometrically nonlinear effects, including the P-D and P-d effects, using at most three finite elements per CFT beam-column
Concentrated plasticity material formulation
Nonlinear solution procedure:
- Mixed incremental/iterative solution, using Newton-Raphson iteration
- Incorporated into frame analysis finite element software

CFT Concentrated Plasticity Formulation

Top

For macro formulation, plasticity has cross section strength as its foundation

Fourth order polynomial equation developed to provide best best fit curve for computational and experimental data
Coefficients vary with D/t and f_c'/f_y
Coefficients calibrated against detailed fiber-based cross section analysis
Accurate for complete range of practical cross section geometries and material strengths

Comparison of Cross Section Strength
Polynomial Approximation to Fiber Analysis
(Axial Force vs. Uniaxial Flexure)

Comparison of Cross Section Strength
Polynomial Approximation to Fiber Analysis
(Y-axis Flexure vs. Z-axis Flexure)

To capture cyclic CFT behavior, a stress-resultant space bounding surface formulation was used
Plastification can be separated into two steps:
- Isotropic hardening
- Kinematic hardening

Isotropic Hardening in Stress-Resultant Space		Kinematic Hardening in Stress-Resultant Space

Isotropic Hardening Stress-Resultant Space Bounding Surface Model		Kinematic Hardening Stress-Resultant Space Bounding Surface Model

Calibration and Verification of CFT Bounding Surface Material Model

Top

Several material parameters require calibration:

Initial and final size of loading surface
Initial and final size of bounding surface
Level of plastic work at which cyclic hardening ceases and strength degradation begins
Rate of change of surface sizes for isotropic hardening
Rate of change in elastic modulus of concrete to model stiffness deterioration

Calibration Procedure:

All calibrated parameters are either:

Constant for all CFT's, or
Vary linearly with ratio of concrete core axial strength to total axial strength of CFT

Verified against over 30 experimental tests conducted by several different experimentalists

Three types of experimental tests, as shown below,
were used to calibrate and verify the CFT formulation

Sample Results from Verification Tests

Top

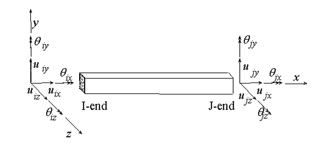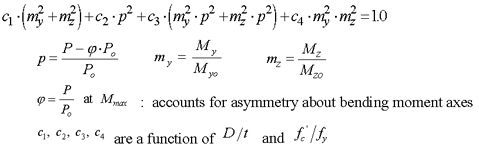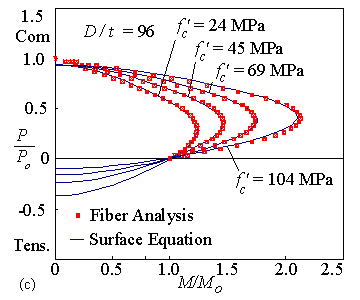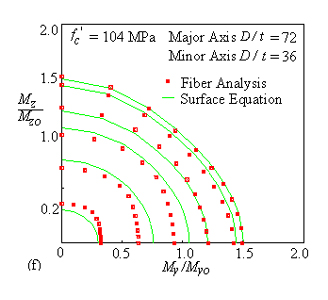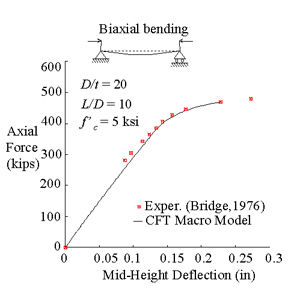
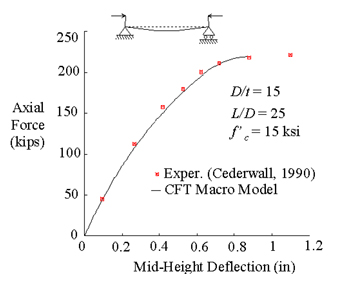
Verification of Macro Model: Proportional Loading, Biaxial Bending, Moderate Length Column, Normal Strength Concrete		Verification of Macro Model: Proportional Loading, Slender Column, High Strength Concrete

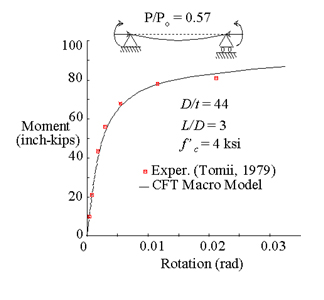
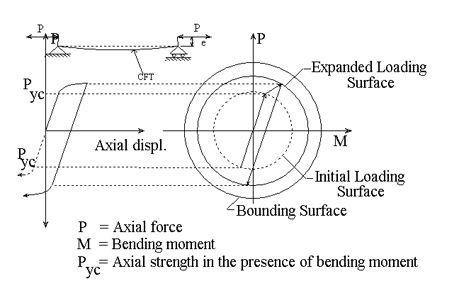
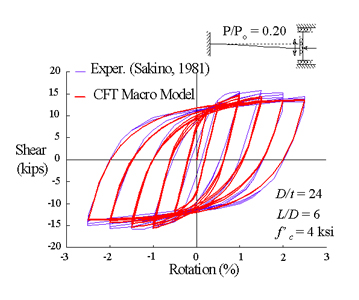
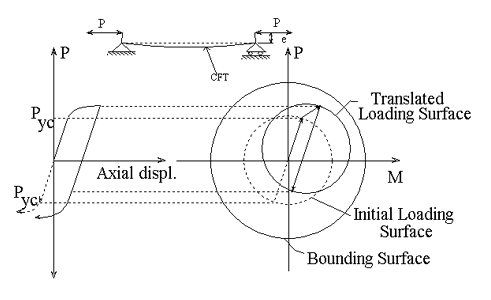
Verification of CFT Macro Model: Nonproportional Loading, Stocky Column, Normal Strength Concrete		Verification of CFT Macro Model: Nonproportional Loading, Stocky Column Normal Strength Concrete

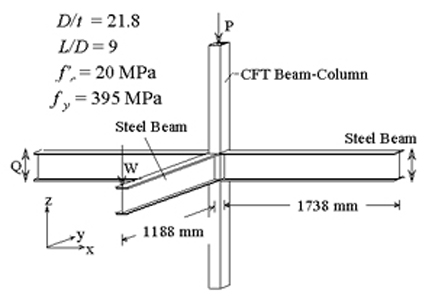
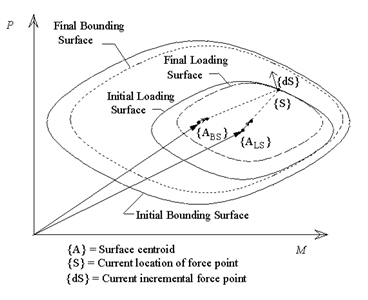
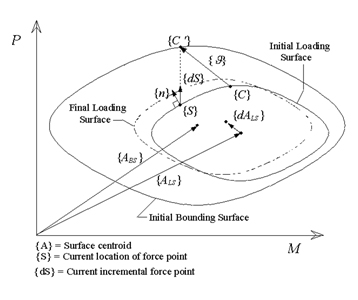
CFT Subassemblage Analysis Verification: Cyclic Nonproportional Loading with Axial Force Plus Bending of CFT Beam-Column		CFT Subassemblage Analysis Verification Analysis model, Measuring Average Shear, Q, versus Chord Rotation, R = (D₁ + D₂) / L

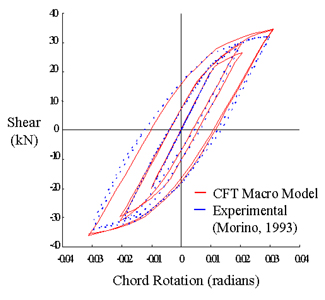
Comparison of Computational and Experimental
Results (R versus Q) for Morino Subassemblage

Applications of the CFT Macro Model

Top

3D static "push-over" analysis for non-seismic or seismic design:
- Simulate earthquake as an equivalent lateral load
- Apply monotonic lad to failure
- Indicates basic nonlinear behavior of structure

3D nonlinear transient dynamic analysis for seismic behavioral evaluation
- Common in research
- Now being incorporated into practice