![]() Introduction to Percolation Theory?
Introduction to Percolation Theory?
Introduction to Percolation Theory
We illustrate percolation with an example.A square lattice is shown in Figure 1a. Imagine the lattice to be infinitely extended in all directions.
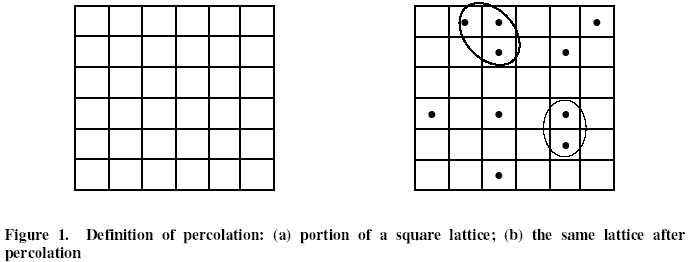
Let's label each square of the lattice to be either in an open state (colored black) with probability p, or in a closed state (uncolored) with probability 1-p. One possible outcome of such an experiment is presented in Figure 1(b). One can observe the formation of clusters, which in the present situation are defined as groups of neighboring squares occupied by a dot.
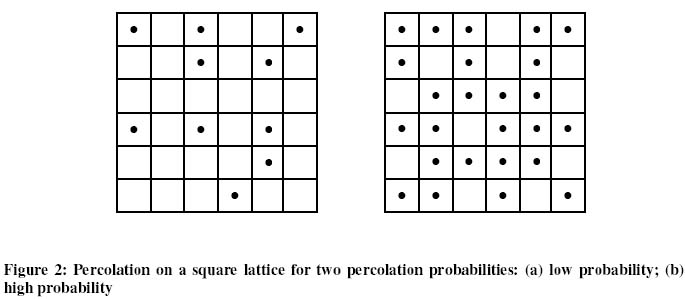
Apparently, the result of percolation depends on the probability with which each site is occupied. Since this is a binomial experiment, the expected number of occupied squares is pN, where N is the total number of squares in the lattice. For a low probability a small number of the squares will be occupied. The result might look like the lattice in Figure 2 (a). On the other hand if the probability to occupy one square is high then a big number of squares will be occupied. The result might look like the lattice in Figure 2 (b). An important feature of the second case is the existence of a cluster that connects the top and bottom, left and right sides of the lattice. Such a cluster is called a percolating cluster and its presence represents a qualitative chance in the structure of the lattice from a disconnected state to a connected one. In the case of an infinite lattice such a percolating cluster is infinite in size. One could extend this percolation phenomenon to higher dimensions, for example the case of a cubic lattice in three dimensions. The basic definition of a percolating cluster as well as the theory behind it are similar.
The percolation model was first introduced by Broadbent and Hammersley1 using the example of a porous stone immersed in a bucket of water. This fundamental question was asked: What is the probability that the center of the stone is wetted? Equivalently, what is the probability that an infinite size percolation cluster of pores exists. Of course this depends on the porosity of the stone, i.e., the probability p.
When such infinite clusters exist? This question leads to the most important and interesting aspect of percolation theory. It involves the threshhold probability, pc. In other words, there exists a critical value for the probability p such that all clusters are finite when p < pc, but there exists an infinite (percolating) cluster when p > pc. As p increases from 0 to 1, such a transition usually suggests an important transformation in the system that is being modeled.
Applications of percolation theory include the modeling
of spread of forest fires, oil exploration, electrical properies of disordered
media, and chemical properties such as gelation and polymerization.
|
|
1 Broadbent, S.R., and Hammersley, J.M., 1957, Percolation processes I. Crystals and mazes, Proceedings of the Cambridge Philosophical Society 53, 629-641.