Introduction to Percolation Theory?
Finite Percolation Network
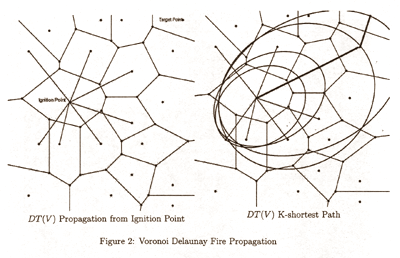
The model of the fire spread network is a finite model on the Euclidean Delaunay Triangulation in E2. There are many possible percolation models of networks on spanning trees and other graph structures. However, the modeling of fire spread on the Delaunay triangulation is unique. Normally, there is a distinction between a site percolation model and a bond percolation model. The Voronoi Diagram represents a site percolation data structure, while the Delaunay triangulation represents a bond percolation data structure. One advantage of the Delaunay Triangulation data structure is that the Minimum Spanning Tree MST(V) is a subgraph of the DT(V).Each Voronoi cell is a state of the stochastic fire spread process. We seek to model how the fire spread evolves over time. The percolation network is finite since we have a number of target absorbing states, roadways, buildings, streams and other barriers which the fire spread network is directed towards. We also want to know when the fire absorbs these objects, since in our evacuation model we need to know the time till absorption as well as the probability of absorption. The Delaunay network and the initiation of its percolation tree is illustrated in Figure 2 for the 20-node network.
We are
interested in the probability that if a fire ignites in a certain cell
that it will reach certain critical cells (absorption states) in a finite
amount of time.